2025, Triangles, and You
Happy New Year! 2025 brings with it many fun mathematical oddities:
It is the last perfect-square year until 2116
2025 = (20 + 25)^2 (^2 means raised to the second power, so squared)
2025 = (1+2+3+4+5+6+7+8+9)^2 (the sum of the numbers from 1-9, squared)
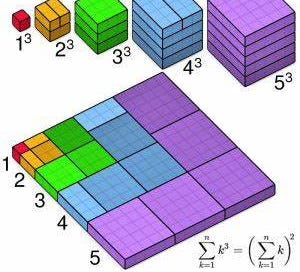
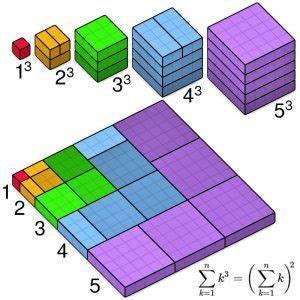
2025 = 1^3 + 2^3 + 3^3 + 4^3 + 5^3 + 6^3 + 7^3 + 8^3 + 9^3 (each number from 1-9 cubed, and then added together)
The last two are actually equivalent. Here’s a nifty visual demonstration:
Also, if you’re not familiar with ‘proof by induction’, this is a great example of how to do one. The way a Proof by Induction works, is that you prove that a fact is true for some number (usually zero or one), and then show that if it is true for n it is also true for n+1.
So it’s like a ladder. Since it’s true for 1, it has to be true for 2. And if it’s true for 2 it has to be true for 3. And so on and so on. Truly neat stuff!
In this case it’s easy to show that it’s true for 1. 1 squared = 1 cubed. So all you need to do to finish the proof is do the n → n+1 part. Here’s a video that goes through the algebra:
The sum of the numbers from 1 to n has a name. They are called Triangular Numbers.
The sequence is 1, 3, 6, 10, 15, 21, 28…
You can see that the difference between the numbers gets one bigger each time.
Triangular numbers get their name from the fact that they can be arranged in a triangle, like bowling pins.
You see this sequence in many games. In Coloretto it is used for final scoring – if you have 3 cards of the same color you get 6 points. Four cards nets you 10 points.
In the game Thebes you are an archeologist trying to find artifacts to score victory points. But you can also get points by collecting Congress cards as you travel through Europe. At the end of the game you score based on the triangular numbers – 1, 3, 6, 10, 15 etc for 1, 2, 3, 4, or 5 cards.
In Sushi Go, the Dumpling cards are valued at triangular numbers based on how many you collect.
This same mechanic is found in the winner of the very first Spiel de Jahres – the terrific Hare and Tortoise – In that game you are racing other rabbits down a track. It looks like a ‘roll and move’ game – On your turn you move forward and do an action based on the space you land on. But rather than rolling dice you get to choose how many spaces forward you will move – but the further you move the more carrots you have to pay. And the cost in carrots is – you guessed it – a triangular number based on the number of spaces you want to move. So if you want to go four spaces, you pay 10 carrots. The reference card in my version goes all the way up to moving 44 spaces, which takes an epic 990 carrots! Here’s a card from another edition that goes up to moving 24 spaces:
In Knizia’s Amun Re there are two features that relate to triangular numbers – the first is purchasing resources. Like Hare and Tortoise, the amount you pay is based on triangular numbers. In addition, when you bid on provinces you can’t just bid what you want -- you have to bid fixed amounts based on a triangular number sequence.
So why are triangular numbers so popular with game designers? When used in a positive way – the scoring in Coloretto, for example - it is an easy way for designers to make the same resource worth different amounts to different players. This introduces complexity and tough decisions into what otherwise might be a simple mechanic. In Thebes, for example, a Congress card may only be worth one point for you, but if your opponent can take it she may score an extra 7 points. So you need to consider putting your own plans on hold to grab it just to deny your opponent. If all of these cards are worth a fixed amount of points that decision would be much simpler to make.
On the negative side, like paying more carrots to move more spaces in Hare and Tortoise, the designer is able to make you decide between distance and time. The most efficient move from a carrot standpoint is to move one space per turn and pay one carrot per turn. But you can’t win by doing that. You need to balance carrots and time – move fast enough to stay ahead, but not so fast that you run out of carrots. Same thing in Amun Re. The increasing cost of resources forces you to balance your purchases and plan ahead. Four farmers this turn is a lot more than two this turn and two next turn.
While not strictly triangular numbers, a similar sequence is used in the classic game Civilization, to very elegantly make resources worth different things to different players. There are a variety of resource rated from 1 to 9 – oil, for example is a 4, and textiles is a 5. In the important trading phase you try to create sets of the same resource. The value of a set is equal to the value of the card times the square of the number of cards you have. So one 4 is worth 4, but two 4’s are worth 4x2 squared – or 16. Three 4’s are worth 36. The great design feature here is that the rapidly escalating values make it worthwhile to trade low value cards for higher cards, while creating a win-win situation. But it also means that you’re never totally sure who is actually getting the better part of the deal.
Oil and Textile cards from Civilization showing the set values on the bottom
I’d like to wrap up this discussion by talking about one more game – Ticket To Ride. In that game you score points when you claim track segments. The sequence of points for claiming segments from 1-6 spaces is 1,2, 4, 7, 10, 15. This is suspiciously close to our triangular numbers sequence of 1, 3, 6, 10, 15. So I was wondering if the design originally used a more traditional triangular number sequence but was changed through playtesting.
I contacted Alan Moon, and let me just quote his reply:
I like to tell people that I don't use mathematical formulas when I design games. But of course, that's not completely true. I know there are designers out there who start with a formula and create the game around it. I think that results in a dry game. I start with a mechanics/theme/bits/whatever and then use formulas only if and when necessary. During playtesting, I'm trying to see how much fun the game is, and not if the math works. So the scoring system of TICKET TO RIDE was made to fit the game, not the other way around. Any relation it has to any sequence is purely coincidental.
My thanks to Alan for taking the time to reply.
So the next time you’re playing a game that uses a triangular or similar sequence, think about what the designer was trying to do, and what impact that has on your strategies and options.