All About That Ace
In 1980 I stumbled across a game called Aces of Aces, a game of World War 1 dogfighting, designed by Al Leonardi. It was unlike anything I had ever seen. It was simply two books, one for the German player, and one for the Allies.
Each had about 250 pages, the bulk of which were dedicated to views outside of your cockpit.
Aces of Aces was a huge staple of my teen years. I used to play it incessantly with my sister whenever we went on a trip. It's the perfect travel game - all you need are the two books. No parts to lose, nothing to spread out if you're in the backseat of a car.
And the way it works is a little magical - and a little mathematical. If I were putting together a list of the Most Innovative Games of the 20th Century, it would definitely be near the top.
I'll start by teaching you how to play.
The Teach
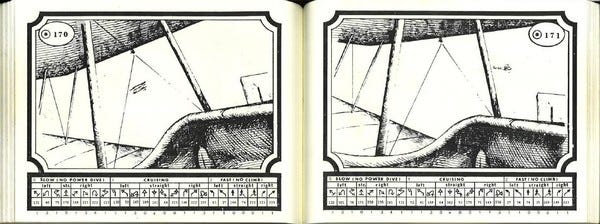
Each player gets a book, and each page shows a particular view outside of your plane. Both players are always on the same page, so you see the opposing plane in the right spot.
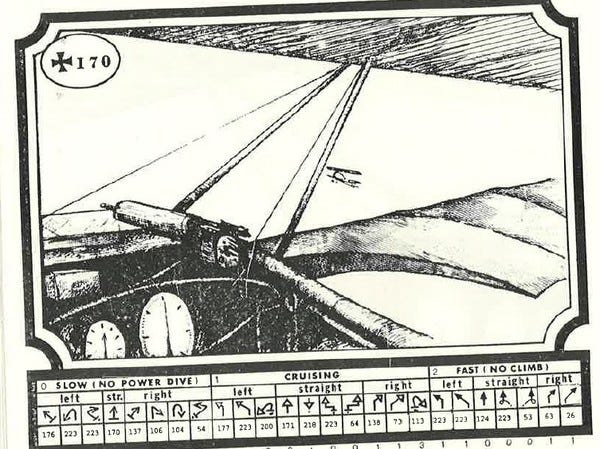
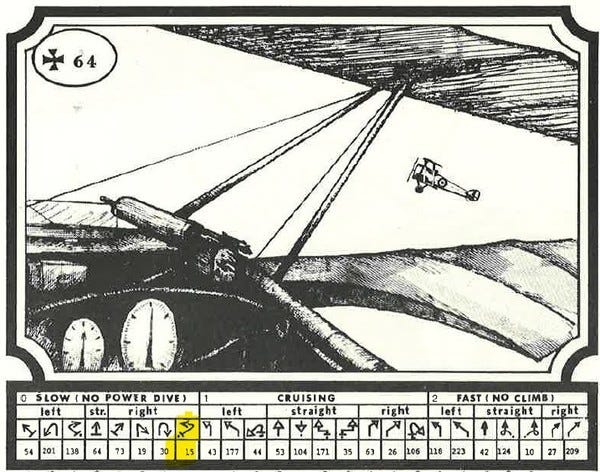
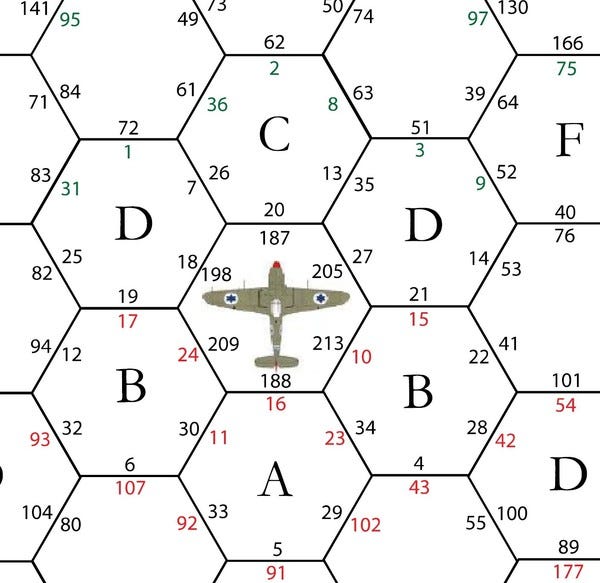
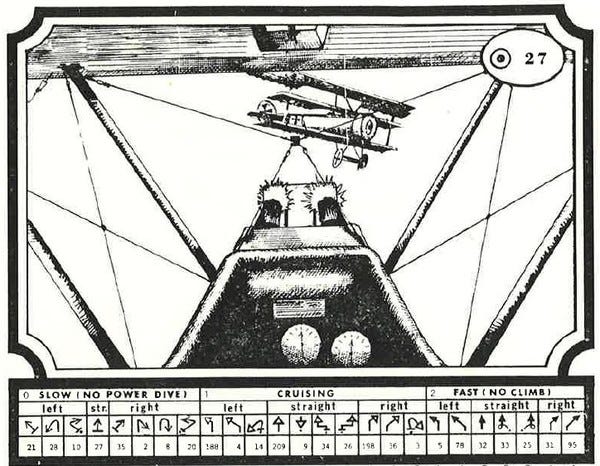
You start the game on page 170. Here's the view from the planes:
At the bottom of each page are the possible moves you can make.
Simultaneously, each player decides on the move they want to make and tells the opponent the number that's shown underneath.
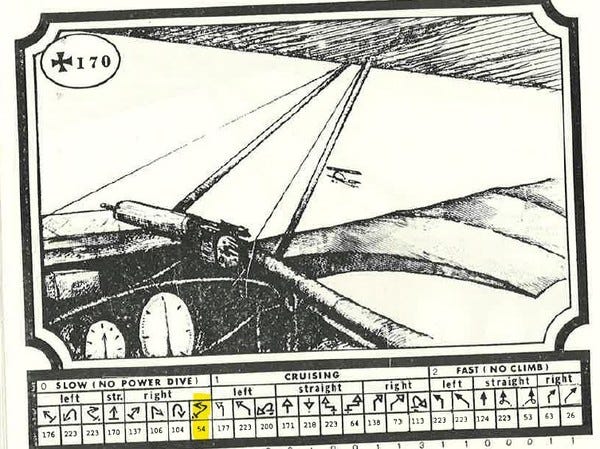
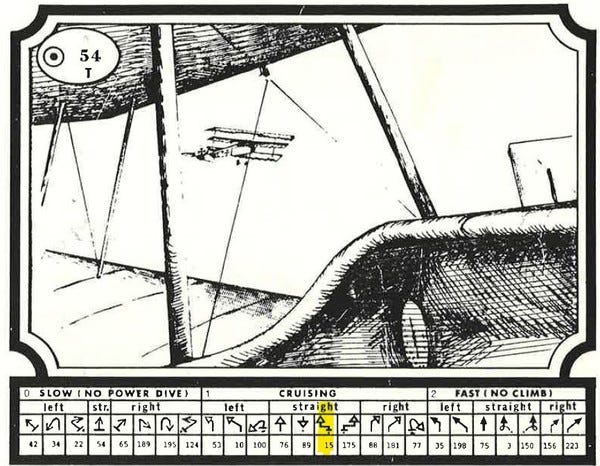
The Germans decide on a slow slip to the right, hoping to get behind the Allied biplane. They tell the Allied player the number under the move, which is 54 (highlighted in yellow, below).
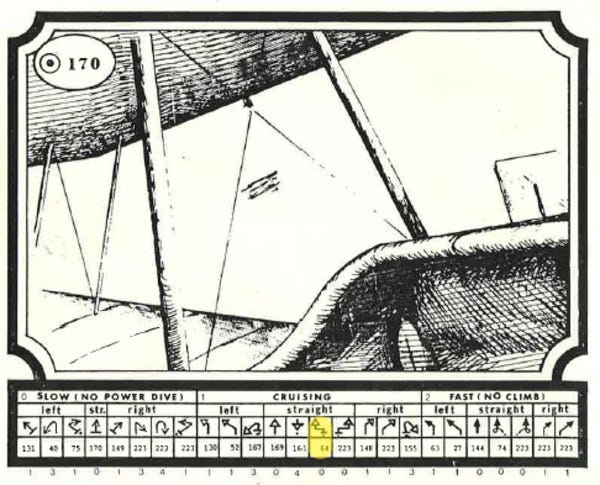
The Allies choose a cruising speed sideslip. They tell the Germans '64', the number under their chosen move.
Now each player goes to the page their opponent told them and looks at the page under the move they chose on page 170. The number under that move is the final page.
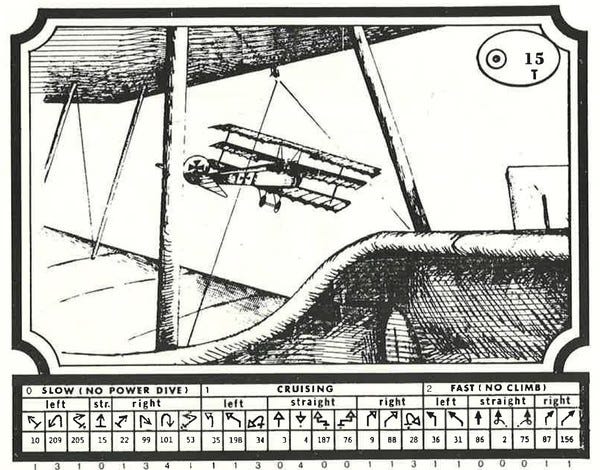
If they do the process correctly, both players will end up on the same page. In this case it's page 15.
And that's the end of the turn! You can imagine the tension and excitement as both players figure out the new position, and the suspense as they turn to the new page. The woodcut-style illustrations also do a wonderful job of placing you in the cockpit and giving a visceral sense of "being there" in a way that Wings of War, Richtofen's War, Blue Max, or any other traditional 'top down' dogfighting board game does not.
You may have noticed that on page 15 of the Allied book there's a 'T' under the page number. That means that the Allied pilot is tailing the German, which gives an advantage. On the next turn the German player has to announce if their move is under 'Left', 'Straight', or 'Right' before the Allied pilot has to make their choice.
Eventually hopefully you will turn to the final page and see something like this:
which causes damage to your opponent. Cause enough damage and win the dogfight, and the game!
If this was a little confusing, trust me that if you are looking at the books while being taught it is really straightforward. You could also check out this video from the designer, Al Leonardi, where he explains it to his grandchildren.
So as I said, this all seems a bit magical. How do the cross references always end up with the players on the same page? How is the movement 'programmed' into the books?
Let's dive into the math. And remember - this game was designed well before computers.
Behind the Curtain
Before I get into the details of how this works, I will say that I think that understanding this takes a bit away from the delight of the game. I'll come back to that later, but consider this a spoiler warning for Ace of Aces. You may want to try playing the game 'unsullied' before diving into this.
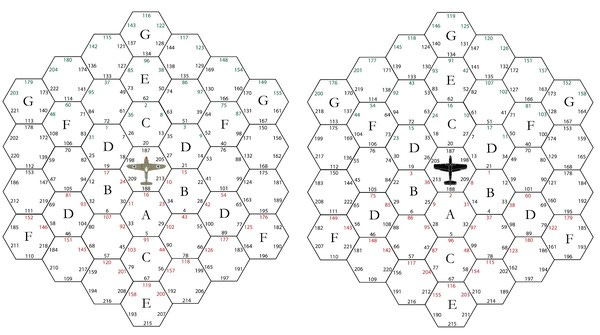
A key thing to understand about Ace of Aces is that it is actually based on a hex grid. Every position that has the players within three hexes of each other is mapped to a page. Here's what I'm talking about:
(Ignore the WW2 planes and the letters - these images were based on Wingleader, the WW2 version of Aces of Aces. But the principle remains the same)
The numbers represent which page is showing that orientation. There are six numbers in each hex since the other plane can be facing six different directions. Let's say the opposing plane was in "A" and facing north. In other words, the other plane is directly behind you! That would be shown on page 16.
The second grid on the zoomed out image shows the point of view of the other plane. In the same example, from the point of view of the opposing plane you are in their hex C, also facing north. It's tough to see, but if you look closely at the full grid on the right you'll that indeed there is a '16' in the expected location.
Incidentally, there are 37 hexes in the playfield (the rings, from inner to outer, have 1, 6, 12, and 18 hexes). A plane can be oriented six ways in each hex, so there's a total of 37 * 6 = 222 images required.
And sure enough, if you get Ace of Aces you'll see that there are 222 primary pages. There is also the dreaded page 223, which you have to go to if the planes are so far apart they are no longer on the same grid together.
The designer created these numbered grids using transparencies. He slid them over each other and entered the same numbers at the right location.
Remember - no computers!
Another factor that helps this work is that there’s no ‘terrain’ in the sky. The relative position of the planes is all that matters. An air battle has what is referred to in geometry as translational and rotational symmetry. If both planes move forward the same distance, the situation is the same. And similarly the relative position of the planes doesn’t change when the entire play field is rotated. If you were trying to bomb a fixed target on the ground, for example, this system will fall apart. The number of pages required then would be unmanageable.
Move It!
So given any orientation of the planes we know what page they should be on. When both planes move, how does that transform their relative locations?
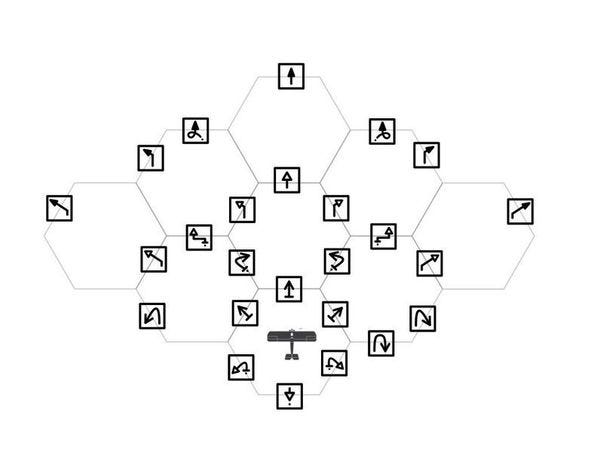
Each move corresponds to moving to a new hex on the grid. Here's a chart that maps the moves to the new hexes.
When you pick a move, you are in essence selecting a hex and a facing. Both players do this. Going back to our double-grids a few pictures above, if you put the planes in the new relative position that will tell you the page number the players should be on.
Getting from A to B
So now, based on the current page number and the moves we know the final page for the players. But how do we get them there?
There are 25 possible moves. So for each move I make, there are 25 pages I might end up on. Each position basically has a matrix that looks like this:
There are 625 (25 x 25) results that need to be filled in. And you need to do that all 222 positions! Remember - no computers. Granted, many of these will go to the dreaded page 223, where the players aren't within range of each other any more. But still, that's a ton of work.
As you may recall, when the players select a move, it sends them to an intermediate page based on what their opponent did. Basically what is happening is that the designer takes a stripe out of the matrix above and places it onto another page. The opponent page # tells them which of these stripes to look up, and then their original move shows where the two moves intersect in the grid.
Time for a Wrinkle
All well and good, but there are a few challenges here besides the sheer magnitude of keeping all these numbers organized.
First, how do you decide what the intermediate page should be? At first it seems like it shouldn't matter. It could be random.
However, the number below each move serves two purposes - sending someone to an intermediate page, and also determining the final page. If we don't organize how those numbers are assigned, could we back ourselves into a corner and have the whole system fall apart as we assign more and more numbers?
I'm not sure. Maybe. However the designer applied a rule which I think kept him out of that morass.
Transformations
In geometry and matrix math (which are closely related) there are transformations you can make that are called the Identity transformation. It means an operation that doesn't change the original value. Adding zero or multiplying by one are examples. In geometry, rotating by zero degrees or translating by the zero vector are others. Identity operations are great to have around for a variety of reasons, and in Ace of Aces one helps keep everything organized.
Let's take a quick look at the move chart again:
See that arrow just ahead of the plane? That doesn't move the plane, and keeps it in the same hex. All of the arrows on the border of the current position hex just rotate the plane - they don't move into a new space. But the one that points up also doesn't change facing.
That's our identity move.
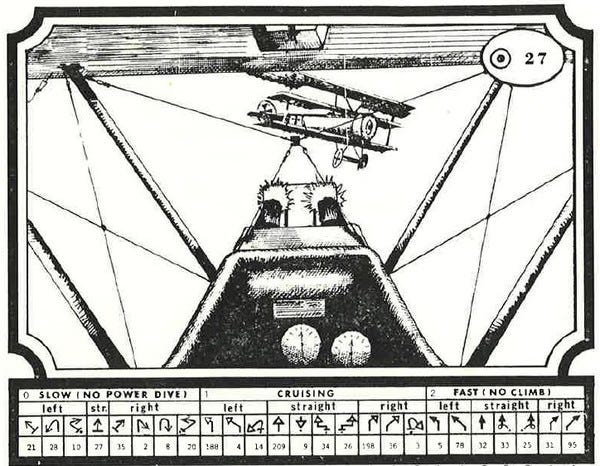
Here's page 27 again. The identity move is the fourth move shown.
It may be a bit hard to see, but the number below that move is... 27. The same as the page number.
In fact, every page has it's own number below that move.
So if both players select that move, the situation remains unchanged.
This is the key that unlocks everything. Let's say we're on page 27. If I pick the Identity move, I send my opponent to page 27 to look up the final page. But that's the page they are already on.
So on a given page, each number below a move sends you to the page where you would go if your opponent does the identity move. This is the key to locking everything down. You still have a lot of work ahead of you to figure out all the positions and numbers, but the task is now manageable, and will be consistent.
Designer Al Leonardi patented the mechanic behind Ace of Aces. Normally I am opposed to game patents, but I think this one is justified. If you are at all interested in the process behind this mechanism I highly recommend you take a look at it. You can find it here:
US4378118A - Action game - Google Patents
The Magic Goes Away?
I am in awe of the audacity of Ace of Aces as a design. It is a towering mathematical edifice. I can't even imagine the leap that convinced someone that making two books like this could actually work. I understand the impetus to design a first-person shooter game before anything like that existed, but I cannot imagine getting past all the roadblocks that must have seemed insurmountable before arriving at a mechanism that actually works.
I love dissecting stuff like this. Most of the time that understanding gives me a deeper appreciation and enjoyment of the system. However I do believe that this is one instance where understanding how the system works takes away from the experience - the experience of flying a biplane or triplane at least.
That you are flying around a hex grid is totally obscured in the game. There is zero indication of it. If you sold this game as a 37-hex map, and told people exactly which hex they would move to based on choosing different moves, it might be fun for a few turns as you try to outguess your opponent. But I don't think it would really hold your interest that long.
Ace of Aces does, and does so brilliantly, but hiding what is going on behind the curtain. You just have the view outside your cockpit, framed by different parts of your plane. You don't feel like you are on a discrete grid. And the moves are barrel rolls, immelman loops, and sideslips. They are way more evocative than just "go to hex A, B, or C and rotate this way".
This system is a masterclass in how a brilliant mechanism can completely transform an experience.
This Far But No Farther
What I have described are the "basic game" rules of Ace of Aces. Included in the package were advanced rules, that included altitude differences, pilot skill levels, cloud cover, and more. And you know what? They absolutely make the game worse. I don't know anyone who preferred the more 'realistic' version to the purity of the base game. Just grab two books and go.
The lesson here for designers is clear - let your core mechanic shine. Don't overburden it with 'realism' for the sake of realism.
Ironically I think I fell into this trap with Super Skill Pinball. I decided that an absolute bedrock principle would be that the game had three rounds - that you get three balls. Because pinball machines give you three balls.
However, the biggest criticism of the game during development was that it sometimes feels too long. I dealt with those concerns during playtest by changing the way certain mechanisms worked (like bumpers), and other tricks to reduce paly time.
Going to two rounds was brought up as an idea a few times, but I dismissed it. Pinball has three balls, and so it was three balls.
Well, in spite of the great reviews in general, that has been the biggest knock. In retrospect I should have considered two rounds more seriously.
However, I did learn my lesson. One of the new tables in Ramp It Up is only two rounds instead of three. And I have a prototype table that is only a single ball! (Editorial note: Since this was written, there have been a bunch of Super Skill Pinball tables released, and very few are now three rounds. Most are only one or two.)
Evaluate all your design decisions carefully.
Aces Wild
The Ace of Aces system was extended into a bunch of other products. There were other WW1 biplanes (and triplanes) that had different strengths and weaknesses. There was also a modern jet simulation, which suffered from added complexity.
And a Star Wars version of course - X-Wing vs Tie Fighter.
Star Wars: Starfighter Battle Book
And even a Dragon Riders of Pern version, featuring dueling dragons!
Other Worlds
The system was extended into a few other directions, notably Lost Worlds and Shootout at the Saloon. I'd like to talk about those, but this newsletter has already gotten way too long. So I'll come back to that in the future.
In the meantime, I hope this inspires you to check out Ace of Aces! If you're interested there are typically used copies of available. There was also a kickstarter a few years ago with a new version.