Balance Part 2

Let's get mathy!

In the last newsletter I talked about balance - the types of balance, and general considerations. This time I'd like to dive into the numeric side of balancing game objects. "How do I balance my cards / abilities / items" is one of the more common questions asked on game design forums, so it is obviously a frequent concern for budding designers.

While there is no absolute formula, there are general principles you can follow.

Step 1: Identify Your Currency

The first step is to decide what your baseline currency is going to be. A currency is a numeric value that everything will be converted to. A good currency will be relatable to all the different factors of your game. Typical examples are money, victory points, health, mana, or a basic resource.

For example, in Dominion, you would probably use money - the resource used to purchase cards - as your currency. In Magic: The Gathering, the resource is the mana required to play cards. In a dungeon crawler it might be money, but it might make more sense for it to be health. Victory Points might also be a good currency in, for example, a point-salad-style game.

The key for a currency is that it should be central to the game experience. Also, the closer the currency is to the ultimate arbiter of victory, the better it is. For example, in Terraforming Mars: Ares Expedition, the design team considered Terraforming Rating (TR) as their currency, and the other resources can be related to that. In Dominion, Victory Points will be a more awkward currency than money, as there are only a few elements that directly give you VP. However, money impacts every turn.

Step 2: Determine conversions

Once you have your currency, the next step is to determine how your different resources and abilities relate to that.

As an example, let's take a look at the game Century: Spice Road, designed by Emerson Matsuuchi. For those of you unfamiliar with the game, there are four resources - turmeric (yellow), saffron (red), cardamom (green), and cinnamon (brown). Ultimately you are trying to collect groups of cubes to acquire victory point cards. Here's are examples:

The spices are ranked from least to most valuable in this order: yellow, red, green, brown. Various game actions let you convert cubes between the different colors. So how do we value everything?

As a natural first step, let's choose the lowest value cube - yellow - as our base currency, and give it a value of '1'. So what should the value of the higher cubes be? That's up to me as a designer, but to keep things simple let's say I simply value red, green, and brown at 2, 3 and 4 respectively.

Let's apply that to the victory cards above. The first is two yellows and two greens, so 1+1+3+3 = 8 - which is the VP value of this card. The right one needs three reds (2 each) and two greens (3 each), which matches the total value of 12. So this is a pretty good fit for what the designer must have been looking at!

So now we can value things that are slightly more complex - the action cards. Here are two starter action cards:

The one on the left gives you two yellow cubes (upper left corner). The one on the right let's you 'upgrade' two cubes to their higher color - so yellow is exchanged for red, red for green, and so on. Brown, the highest level, cannot be upgrade.

Based on our 1/2/3/4 valuation, these cards are each worth '2'. Two yellows are worth two, and each upgrade is worth one.

Here are more actions:

The arrow means that you convert the cubes. So the first card would exchange three red cubes for two brown cubes.

See if you can figure out the value of each of these cards.

From left to right, the top row is worth 2 (3 reds = 6 → 2 browns = 8), 3 (gain a yellow plus a red), and 2 (2 greens (6) → 8).

The bottom row is 4, 3, and 2.

You can see from these examples that the designer deliberately put in 'unbalanced' cards. So is the game itself unbalanced? No. Having variation like this gives texture to the deck and reduces some decision making. For example, maybe most of my cards want red cubes as inputs. Then the 'gain a red and yellow' might be more valuable to me than 'gain a green and yellow'.

Even the victory cards aren't strictly sums of the cube values. Here are two other cards:

On the left card, the sum of the cube values is 18, but the card value is 20. On the right card, the sum is 8, but the value is 9.

Step 3: Determine the value of Intangibles

This brings up another consideration for valuing cards - intangibles. These are factors that aren't directly indicated on the cards, but factor into what they can or can't do. For example, in Spice Road the victory cards that require three or four different color cubes give one or two more Victory Points, as in the example above. Matsuuchi determined that it was harder to get multi-colored sets, so the value needed to be slightly higher to compensate.

Here's another example of an intangible, adapted slightly from the videogame deck builder Slay the Spire.

Let's say my baseline card requires 1 energy to play and does 6 damage.

Now I have another card that costs 1 energy to play but does 9 damage. This card is clearly superior to my baseline card.

But what if I create a card that does 12 damage, but costs 2 energy to play?

It seems at first that this card is equivalent to the first. 6 damage for 1 energy is the same as 12 damage for 2 energy.

However various intangibles may impact this. First, since this is a deck builder, most of the time there is an inherent advantage to having fewer cards in your deck. So have one 2/12 card is better than having two 1/6 cards. You will see it more often, and your draws will be more consistent overall.

However, what if you have three energy to spend each turn? Then having two of the 2/12 cards may not be as good as four of the 1/6 cards. I could only play one 2/12 card when I could play three 1/6 cards.

Or maybe there are other synergies in my deck that increase the value of two 1/6 cards over a 2/12. For example, maybe I have a card that gives me block equal to the number of cards in my draw pile. Now having more, lower value cards, will give me more block than one more powerful card.

Ultimately this means that there is no clear rule about the value of an object in a game. And this is a very good thing. In fact, I would argue that this is the essence of good game design. Giving players tools that are more valuable in one situation and less in another, or having combos that elevate the value of all the elements, or value varying depending on what opponents are doing - these are all very good features for a game and what will keep people coming back for me.

Perfect balance can only be achieved by removing these more complex interactions, but that also removes the interesting bits.

Valuing Combos

Sometimes you will be called upon to value a combo. This can be challenging to do. Let's say you have a two-card combo. If you can play both on the same turn they are a value of 10. But if played individually they have a value of 3.

How do you value that? Does it make sense to just value each card at 3, and if players get the combo, great for them? Or value each card at 5 figuring the combo would be overpowered if it only cost six?

Or value each card at 4? Or some other middle ground?

Ultimately testing will let you know, but the key factor to look at here is how likely is it that the combo will happen.

If the combo is very simple to put together, I would tend to value it closer to the 10 level - probably not at 10, but not as low as 6 either.

But if the combo is less likely to come together, the value of each piece can be dropped accordingly.

For example, in Dominion if you want to do a two-card combo you need to draw both in the same turn. This depends on the size of your deck, additional card draw that is available, and so on. But you can determine a reasonable number. For example, in a 15 card deck with some card draw you will draw 2-3 hands per shuffle, so you have a 11% - 25% chance of getting the combo (1/3 squared or 1/2 squared). This can help guide you about the power.

By contrast, Quarriors is a dice-pool building game. In order to get a combo you need to draw the dice together, but then also roll the combo sides. So now maybe your combo is in the 5% chance of happening range. In this case you can make your combos really powerful and exciting, since they won't happen that often.

You also may want to take into consideration the other players. Will they be acting to stop players from getting particularly powerful combos? How much might this decrease the chances of the combo occurring?

Valuing Time

Another consideration for balance is the time factor. How many times will an item get used before the end of the game? Cards that you get early can be used many times. Cards that you get towards the end may only be used once or twice.

In some games the timing of when you get cards is more explicit. In Through the Ages, for example, the deck is broken up into four 'Ages', with cards specifically in each one.

Cards in the final Age will not be used as often. How is that compensated for in the design?

Here are what the four resource-producing cards look like:

The order (as you may surmise) is Bronze, Iron, Coal, Oil. The values each produces are 1, 2, 3, and 5 respectively (bottom center). That '5' for Oil is strictly to balance against the reduced amount of time you get to use it.

In Terraforming Mars: Ares Expedition, the designers have noted that the value of each card for balance purposes was weighted by how many times it would probably be used in a game, which is based in large part on whether the card is 'normally' played early, mid, or late game. It was scaled based on when it was expected to be played. Cards that, for example, are scaled around being played in the early game will be below the curve if they are played late.

Again, though, combos and synergy will help offset this, and enhance a card's value.

Granularity

Another consideration for your 'base currency' is the granularity of the metric. If you are trying to balance something, and only allow for cost 1, 2, or 3, you may have a situation where 1 is too cheap but 2 is too expensive.

In this case you can either just deal with the variance (which is what games like Slay the Spire do), or you can increase the granularity of the resource - double all the values so that your scale goes from 1-6 instead of 1-3.

The trap here is that you usually don't want your numbers to get too big. This makes math more difficult and can be confusing.

This problem is particularly prevalent in miniatures games, where players decide on their 'army lists' and can choose units up to a certain point value.

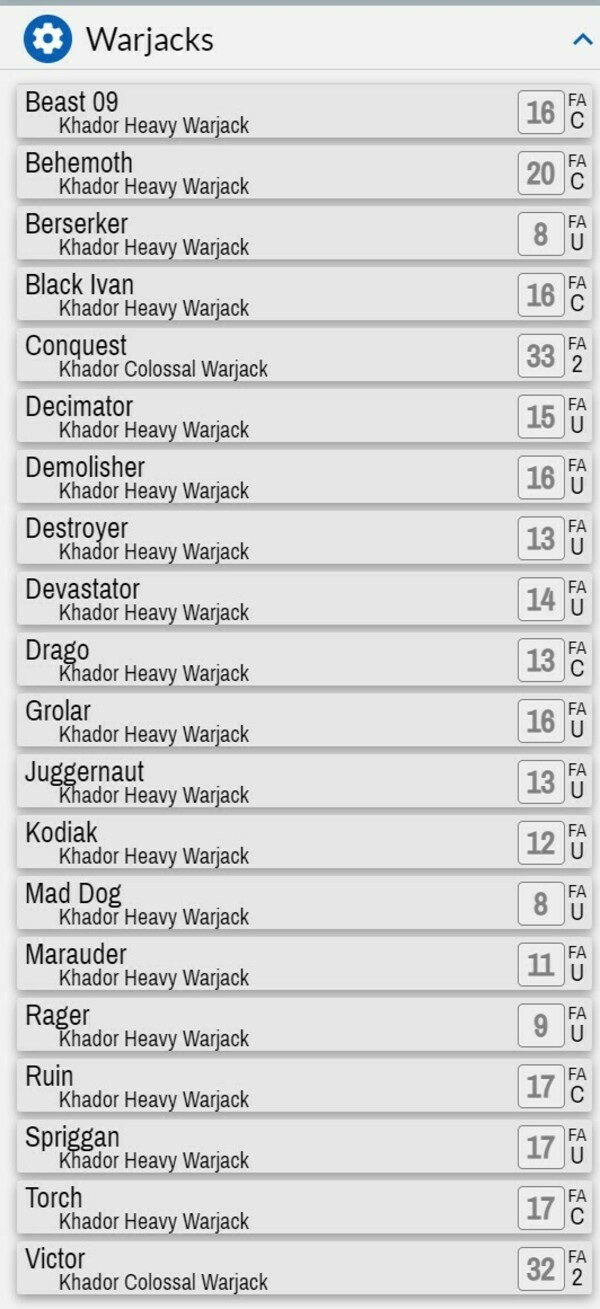
Here, for example, are the costs for the Warjacks from the Khador faction in Warmachine:

A Juggernaut costs 13 points, a Kodiak 12, and a Marauder 11. Is that a meaningful distinction? Maybe. But probably not. It also means that players must spend extra time before the game developing their lists and figuring out the best combos while staying under a cap. However, for some players this is actually part of the fun and attraction of these types of games.

I can't even begin to try to figure out if 13/12/11 is really the 'right' cost for these mechs. An interestingly-designed game will make the 'value' of a unit dependent on a host of other factors.

Designing for Experience Levels

One last factor to consider: Do you balance around how an experienced player can use a card or combo? Or a novice player? I touched on this a bit in the last newsletter, around my game The Expanse. In that case I designed around experienced players which led players to believe that the more technically difficult factions were underpowered.

You can run into the same issue with a single card or item. New players may not realize how incredibly powerful a card is. Do you cost it based on the perceived value to novices, or the actual value to experienced players?

As an example, here's the Corruption card in Slay the Spire:

This card reduces all Skill cards in your deck to zero cost, but when you play them, they are removed from your deck for the remainder of the battle. There are three types of cards - Attacks, Skills, and Powers, so this will affect a big chunk of your deck.

Most beginning players are scared of this card. It costs three, and you will rapidly run out of Skill cards. They would probably be more inclined to play it if it cost less, but at that value it is too steep.

Experienced players realize the true value of this card and that it is probably costed correctly.

As another example, in our game Dragon & Flagon you have various action cards that can give you Reputation if they succeed (victory points, in essence). We found that players were shying away from the flashier, more fun and exciting actions in favor of dull but more predictable actions.

To counteract that, we really ramped up the Reputation rewards for the flashy moves we wanted players to choose and kept increasing it until we got the flavor we wanted.

At this point I am convinced that these moves are 'balanced' for beginning players, to try to get them to do those fun moves, but that experienced players will be able to exploit that to their advantage (by completely eschewing the basic moves). However, since D&F was aimed at raucous play, and chaos is more important than balance, we purposefully shaded it in that direction.

Conclusion

The bottom line is that perfect balance is a white whale that can't really be achieved. And honestly, it's probably not worth achieving anyway. The tools and techniques discussed here will hopefully get you closer to a good spot but this is another example where you should trust the playtesting and your instincts more than the math.