Effective But Boring

I’m working on a new game design with my kids (it’s great to have the band back together!) that features special player abilities. While brainstorming abilities I came up with a fun idea. Here’s the ability:

When rolling a die (at various points you roll a D6), you do it secretly. You announce what you rolled, and you can lie. The other players can just let it pass, or they can accuse you of lying.  If you were lying, treat the roll as a zero. If you were telling the truth, the roll counts double. So if you say it’s a ‘five’, and your opponents accuse you of lying, it will either count as ten or zero depending on whether you were truthful or not.

We played a game with it, and it made for some fun moments. My daughter played that ability, and I caught her out a few times, but she also got some big ‘doubles’ in. It was fun but not overpowering. Also, it introduced a nice bit of yomi into the game (“Yomi” is the feeling of trying to outguess what your opponent will do – think the Princess Bride iocane powder scene).

But even though it worked in playtests, something about it was bothering me. Was doubling the right thing to do? Was it too powerful? Not powerful enough?

More importantly, was there an optimal strategy you could use, on either side?

Feel free to think about it yourself before moving on. How would you use this ability?

The Algorithm

I came up with this simple strategy:

If I roll a 1, 2, or 3, lie and say 4, 5, or 6 respectively (so add 3 to the result). If I roll a 4, 5, or 6 tell the truth.

Using this strategy, 1/3 of the time I will say 4, 1/3 of the time I will say 5, and 1/3 6. And 50% of the time I will be lying.

This strategy also makes lying ‘easier’, since I am just using an algorithm (a definite rule). I don’t have to hesitate to decide what I will say the roll is.

So let’s say my opponent never accuses me of lying. What does that look like?

My ‘rolls’ will be 4, 5, 6, 4, 5, 6, or an average of ‘5’ per turn.

What if they always accuse me of lying?

My rolls now will be 0, 0, 0, 8, 10, 12. If you add those numbers together you get 30, so the average is also ‘5’ per turn.

What about if the opponent tries a different strategy? Maybe they only accuse you of lying when you say 6?

Rolls: 4, 5, 0, 4, 5, 12. Average of 5

What if they only accuse you of lying when you say ‘4’?

Rolls: 0, 5, 6, 8, 5, 6: Average of 5

This strategy does the same thing regardless of what your opponent does. It makes no difference what they do.

The Nash Equilibrium

In game theory this is called a Nash Equilibrium, as it was first discovered by the father of game theory John Nash. If a strategy is ‘optimal’, anything the opponent does will either not change the outcome (as in my die example), or make things worse.

Nash strategies can either be ‘pure’, which means they are deterministic, or ‘mixed’ which means you choose different options a certain percentage of the time. My 4/5/6/4/5/6 strategy here is a pure strategy. In the same situation you always do the same thing.

Rock, Paper, Scissors is an example of a game with a mixed Nash Equilibrium strategy. You should randomly pick each 1/3 of the time. If you do, no matter what your opponent does you will win 1/3 of the time, lose 1/3 of the time, and draw 1/3 of the time.

Nash proved that any game where players have a finite number of options has a Nash Equilibrium, although realistically for most games it is very difficult to determine that without serious computing power, if at all.

One area where the Nash Equilibrium strategies have been making inroads is in poker. The new trend in poker is Game Theory Optimal Poker strategy, also known as GTO.

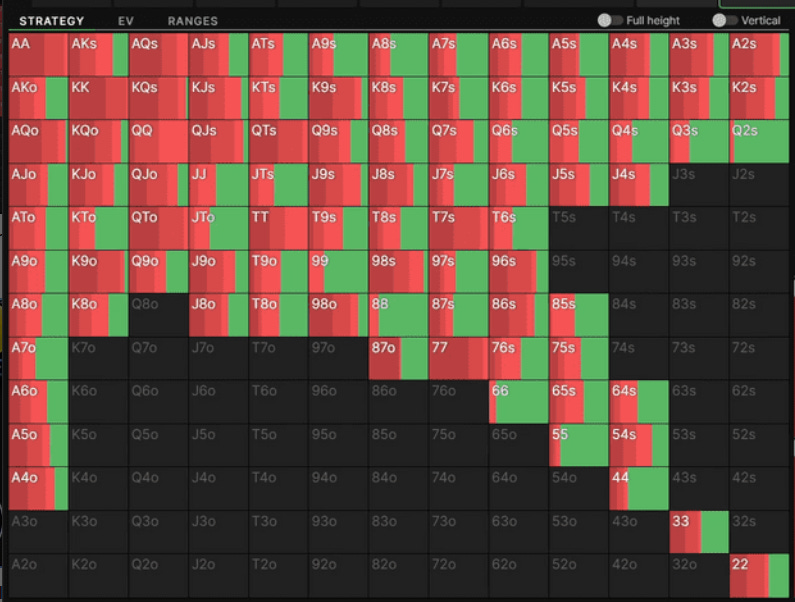
Students of GTO poker study charts like this, that lay out the 169 possible starting hand combinations (treating all ‘suited’ combos the same and ‘unsuited’ combos the same), and what you should do based on where you are sitting relative to the dealer and what your opponents have already done (called or raised).

Red means raise, green means call, black is fold. You’ll see that for each hand there is a certain percentage of the time you should raise vs calling, although a few (like pocket Aces) have you raising 100% of the time.

Let’s say the GTO play in your situation is to raise 25% of the time and call 75%? How do you generate random numbers at the poker table? Humans are notoriously bad at this. One subtle way to do this is to wear a watch with a second hand. In our example you may decide that if the second hand is between the 12 and 3 you’ll raise, otherwise you will call. Then glance down.

But Is It Fun?

Part of the reason I enjoy playing poker is figuring out whether someone is bluffing or not. GTO takes the ‘human factor’ out of the equation. Does it make poker less fun?

In my opinion, no. I don’t believe a person is capable of playing fully GTO poker. There are just too many situations, and ultimately you have to go with heuristics, or go with your gut. So there’s still room for staring into the eyes of the person across from you to figure out if they’re trying to slip something past you, or actually have the goods.

But in general, playing a Nash Equilibrium strategy is boring. By definition there are no decisions. You just follow the plan, randomizing as necessary. And it’s frustrating to play against, because nothing you do makes a difference.

In our game mechanic, if someone uses the 4/5/6 strategy it will still be balanced. You will, on average gain a +1.5 to the die (average of 5 instead of 3.5). And that is actually in line with the other special abilities.

But it’s decidedly un-fun.

However - do we know that people will use that strategy? It’s not obvious. We went through a few playtests, and no one figured it out. They were just playing the ability ‘as intended’.

In my opinion, no. Particularly in the current connected age, if one person figures out that strategy, it will spread like wildfire. You can’t include a time-bomb like that in your game. You can’t have a strategy that’s simple, effective, and boring.

In the end, we ditched the doubling and changed it so that you get a +2 bonus if you are falsely accused of lying. There’s still a Nash Equilibrium strategy - there always is, remember - but it makes it a tough-to-calculate mixed strategy, so people won’t use it. The deadly part of the 4/5/6 strategy is that it’s very easy to understand and execute.

When you’re designing, look for these types of situations. I’ve seen them in published games, where a simple, deterministic strategy is the optimal way to play. It’s not a good thing. The warning sign is when the expectation value (the ‘average’ in my die roll mechanic) is easy to calculate.

The Universe Explained with a Cookie

My new book, The Universe Explained with a Cookie has been out for about a month, and I’ve gotten great feedback! If you’ve purchased the book through a major online retailer like Amazon or Barnes & Noble I would be most appreciative if you could leave a rating or review. They are hugely important for having the book show up in search results (speaking of algorithms!).

Thanks for your support!