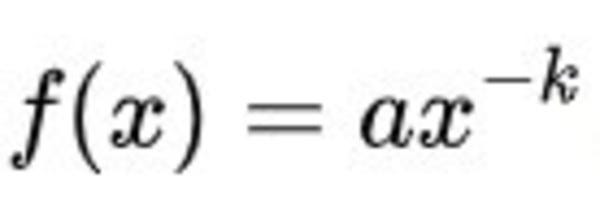Power Laws and Game Design

In this week's episode of The Dice Tower I talked about Power Laws. For this first issue let's dive into it in a bit more depth than I was able to in the show. (Note - of course this is an old post. The Dice Tower podcast has ended, in case you go looking for this).

First, a quick primer on Power Laws for those of you that did not get a chance to listen to the segment. A power law is a relationship between two values that can be described by this equation:

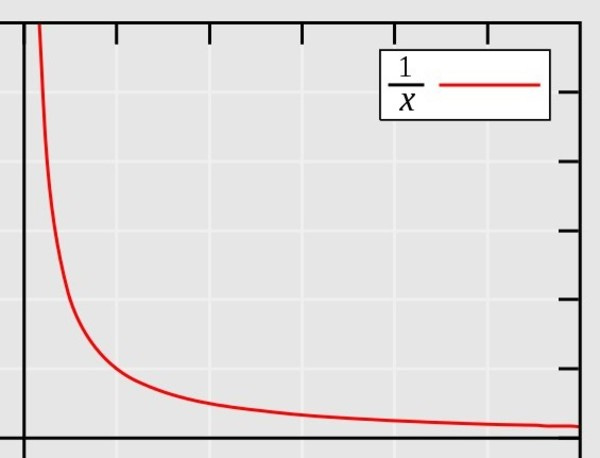
It looks a little scary, but it's not really. The simplest form is when both ‘a’ and 'k' are 1 which turns this into y = 1/x (which is the same as x raised to the negative-one power). A graph of 1/x, it looks like this:

The key idea is that there's a lot of something at small values, and not so much at big values. At values above one the graph drops down slowly. x = 2, y = 1/2. If x = 10, y = 1/10. But as you go below one it rapidly rises. x = 1/2, y = 2. If x = 1/10, y = 10.

There are a lot of natural phenomena that follow this general curve. For example, if you look at the number of earthquakes of different magnitudes (strengths), it has this form. There are many, many earthquakes at magnitude 2 or less, but only a few at 6+. Here's a chart that's rotated sideways that shows this:

There are a million magnitude 2 earthquakes a year, but only a hundred and fifty magnitude 6, and two that are magnitude 8.

So what does this have to do with games? Well, we are very used to seeing power law systems in nature. We find them aesthetically pleasing. For example, here is an image of a tree:

The number of branches of a given length follows a power law. There is one really long 'branch' (the trunk), and lots and lots of very small branches -the twigs, with decreasing amounts of intermediate sizes.

Many games do not have a power law structure - they are flat. Perhaps cards all are the same strength levels, or there are equal numbers at different strengths. Or the VP you gain from different actions is pretty tightly constrained, and in a small range.

I think a lot of games would benefit from trying to have Power Law-style elements (calling it 'PL' from here on out). Again, the basic idea is that most of the time the 'baseline' (or lowest) thing happens, and as something gets better it happens less often.

Let's take a look at some areas you may consider adding PL elements.

Power Law via Components

One way to add PL elements is through the components. The Great Dalmuti for example, has cards numbering from 1-12, with that many of each. So twelve 12's, eleven 11's, and so on, down to one 1. And the 1's are the most powerful cards - so when you pick up your hand and see a 1, or maybe one of the 2's, it's fun and exciting - both because it's a relative rarity, and because you know you definitely have an edge over the other players.

With just a regular deck of cards the value distribution will not be a PL. In Bridge, you will have an Ace most hands. A normal deck of cards does have a PL element for the distribution of cards, though. Only rarely will you have no cards of a suit - so that can bring some of that same feeling. But building it into the component distribution gives the designer more control over the statistics.

Power Law via Randomness

PL can also be introduced through randomness. This is related to a talk I gave at GDC about White, Brown, and Pink Noise:

"Pink Noise" relates to the level of 'correlation' in the noise. In other words, if I know what happens at time t, how much does that tell me about what happens at time t+1. In Pink noise, most of the time you know a lot - what happens at t+1 is very close to t. But sometimes it jumps more, and every once in a while it jumps a lot.

There are a few ways to do this with dice:

A normal 2D6 or 3D6 distribution, except that the 'tails' are the best results (going both ways - so a 3 or 18 on 3D6 would be the best).

Variable die faces: The die faces can be varied to generate a typical PL curve. For example, on a D6 you could have three 1's, two 2's, and one 3. A d20 would give you even more opportunity to create this type of curve.<

Dice Difference: The result is the difference between two dice. For 2D6, that skews heavily towards a zero or one result (fully 16 out of 36 possible results) and 2 out of 36 'five' results (on rolls of 1/6 or 6/1). This distribution actually gets flatter as you go to larger die sizes. But combining this with variable die faces might prove interesting.

However in all of the above there's still a 'best case' scenario. If you want an open-ended top end you need to go to...

'Exploding' dice:

You get a reroll on high numbers. For example, in Uncharted Seas you roll a bunch of D6's. For each roll of 4 or 5 you score a hit. For each 6 you score two hits, and also roll the die again, possibly scoring another hit or two, and maybe generating another reroll.

This leads to battles where the attacker can get way more hits than expected, as sixes keep coming up. And there's always a chance that even the weakest unit can take down the strongest battleship. There is no theoretical upper limit on the number of hits that the attacker can get.

And that's exciting. When it happens it generates great stories. That's the power of a PL mechanism.

A consideration though is how often the 'rare' event (sometimes called a Black Swan event) happens. You don't want to make it so unlikely that the payoff doesn't match the frequency. For example, consider Quarriors. It's billed as Dominion except with dice instead of cards. The promise of the game is that you draft dice that have synergy. However, in my plays I found that when I tried to get dice that synergized together the combo was just too rare. First you had to pull the dice from the bag at the same time, and then you had to roll the right sides.

I found it really frustrating with how rarely my combos triggered, particularly because they weren't incredibly powerful.

Of course there are exceptions to the rule. One of my absolute favorite rules in games is the Bene Gesserit prediction victory in the original Dune. At the start of the game the BG player writes down which player they think will win, and on what turn. If they are exactly correct they win instead.

In the dozens of games of Dune I've played I've only seen it happen once. However it's such an amazing moment - and so thematic - that just knowing that unlikely 'black swan' is out there adds tremendously to the game.

Power Law via Cascades

A classic example of a power law is the sand pile. If you drop grains of sand on top of a large pile of sand, occasionally there will be 'avalanches' where grains slide down. Most of the time it will just be a few grains, but occasionally the avalanche will be pretty large. (Actually whether this actually happens or not in sand piles is still being debated, but mentally you get the picture).

This type of 'cascade' mechanism can be very powerful in games. The game can approach a 'critical' state where small moves can have big consequences.

A physical example is the Coin Pusher machine. In these games you put a coin or token in the machine and it pushes it onto a platform with lots of other tokens. Any that pushed off the edge you get to keep.

Via Appia directly mimics the idea of the coin pusher with its quarry. You insert a resource disk at the narrow end, and push it in. You get to keep any discs that fall out the far edge. The flare of the sides is a clever physics trick that makes the result of inserting a new disc more unpredictable.

Beyond physical implementations, there are other more subtle ways to implement PLs. Pandemic's Infection/Outbreak system. If there are three disease cubes in a space and fourth needs to be added, instead you place a cube in each adjacent space. This can lead to further outbreaks, triggering a chain reaction. A single cube in the wrong place can explode the board and rapidly lose you the game.

Another is the child's game Dots and Boxes. For those few of you unfamiliar with the game, each turn you connect two adjacent dots. If you close off a box you mark it with your initials and get to go again.

Dots & Boxes is a game of brinksmanship of a sort. You don't want to leave your opponent with a box to close, but eventually someone will have to do so. And since both players have been avoiding setting up their opponent any move that does so usually doesn't just result in a single box - it results in a chain of them getting filled in. Advanced strategy in the game consists of manipulating these 'blocks' so that you have some small ones you can toss to your opponent and get the larger ones for yourself.

Another way of expressing a PL in a game is through how victory points are awarded. Many "point salad" games distribute lots of small amounts of points, in fairly even amounts. The knock on these games is that there is not much to differentiate choices - if everything gets you a point, that diminishes the quality of one option over another. There are a plethora of games where points are earned in a narrow range.

Personally I like games where there's the chance for big scoring plays, particularly if you can set something up over several turns and then the plan comes together for a big score. For me, lots of low scoring turns punctuated by occasional big scores makes a game fresh and exciting.

My old favorite Through the Ages does this well. Most of the points (culture) you accumulate are done slowly, turn after turn. You accumulate a few points each round depending on the buildings you have. But wonders and wars give you a chance for a big payday. I've seen 40+ culture swings due to wars. They don't happen often - PL-style - but when they do they are memorable.

Power Law via Decision Space

The last thing I'd like to discuss is modeling the entire decision space of a game as a power law. Most of the games we play have some player decisions. And those decisions will vary in importance. Sometimes the decisions will be inconsequential, or any decision equally good. But sometimes the decision will be a critical point in the game that will determine victory or defeat. And there are decisions of all importance levels between these.

One option is for every decision to be equally important. However, I would propose that a PL distribution of decisions is best. If every decision is incredibly important I find it fatiguing. It also makes it harder to improve, as it can be more challenging to know which decisions led you astray.

By having mostly inconsequential decisions, punctuated by some moderately important decisions and a few critical choices the game has a much more dynamic texture. It allows the player to have a rhythm of how the engage, and a chance to recharge and put plans together that culminate in a key turn.

I also think that these key decisions shouldn't always come at the same time in the game - or maybe not always be obvious to the novice player. Knowing which decisions are truly important, and which can not receive as much attention can turn into a critical skill differentiator.

To wrap up - consider incorporating power law dynamics into your design. It can be overt, like a component distribution, or more organic, like a decision space. However you do it I think it will result in a game that feels more alive and more engaging.