Mathematicians made a big discovery this month (March 2023 if you’re in the future - hope it’s going well there!) - they have constructed an Einstein tile. This is a single tile that can tile the plane, but in an aperiodic way.
To unpack that definition, let’s go back to the 1960’s. Mathematician Hao Wang was working on the problem of tiling the plane with dominoes. Tiling a plane means completely filling it with shapes. We’ve known for a long time that are only three regular polygons that can be used to tile the plane – the triangle, the square, and the hexagon. (A “regular polygon” means that all the sides are the same length, and the interior angles are the same.)
You can make a grid of these shapes that extends to infinity. And that’s why those shapes – squares and hexagons in particular – constantly show up on our game boards. It is very easy to drop those shapes on top of the board and have them regulate movement, or shooting, or whatever you’d like.
Now there are actually an infinite number of shapes that can be used to tile the plane that aren’t regular polygons. Rectangles are a trivial example. The artist MC Escher was a huge fan of using shapes like lizards to tile planes in his drawings.
Planar tilings can also be accomplished through multiple tiles. Many bathroom floors are tiled in collections of different sized square tiles, or squares and rectangles, or even octagons.
All of these tilings have one thing in common – they are ‘periodic’. This means that you can shift the whole pattern over and the tiles will line up on each other. This is called ‘translational symmetry’. You can translate the pattern onto itself, and it repeats infinitely.
For example, if you go back to the lizard pattern above, you can see that if you shift the whole pattern diagonally up or down it will move on top of itself. Just match the white lizard, for example, to another white lizard facing the same direction. The whole pattern will translate onto itself.
Mathematicians assumed that any tiling with a fixed number of tiles had to be periodic. There was no way to fill the plane with shapes and have the pattern never repeat.
OK – so back to Hao Wang. He was working on a problem with square dominoes with different colors on each side, and when the dominoes were placed down the colored sides had to match up. Think Carcassonne tiles. He was taking an arbitrary set of Carcasonne tiles, and asking the question – Can I tell whether or not these tiles will let me completely tile the plane infinitely in all directions?
He wasn’t able to figure it out exactly. However, he was able to prove that if the tiling is periodic you can always figure out if the set of tiles will in fact cover the plane. He thought all patterns must be periodic, so he figured this was as close to a proof as he was going to come.
Five years forward – 1966. Robert Berger is able to prove that you CAN’T tell for sure if a set of Carcassonne tiles will cover the plane. Therefore using Wang’s proof, there must be a set of tiles that fill the plane aperiodically – in other words, WITHOUT repeating a pattern. Berger was able to find a set of 20,000 different tiles that would work. Unwieldy, but a breakthrough.
People kept working on aperiodic tiling, and in 1973 the brilliant physicist and mathematician Roger Penrose got it down to two tiles. With two specially-shaped tiles you can infinitely cover the plane, and not be able to shift the pattern onto itself.
These patterns typically display five-fold symmetry, and are fractal in nature. They look like they are repeating, but don’t quite. If you’ve never seen a Penrose Tiling you should check one out. They are very cool, and I’ve always wanted to buy Penrose tiles to cover my bathroom floor. In fact, I tried to do this for my recent bathroom remodel, only to find out that Penrose had patented his tiles (boo!) and so no one was making the commercially, even though the patent has expired. I think the person laying my tiles also would NOT have been happy with me.
My son went to Carleton College, and they have a famous Penrose tile mosaic on the floor of the math department. I always liked to visit it when we were there.
You can clearly see the pentagonal nature of the tiling in this picture.
OK – jumping forward in time to 1982. Dan Shachtman is doing diffraction experiments on crystals to understand their shape – and saw a five-fold symmetry pattern, which no one had ever seen before. A few more years of research convince him that the crystal is actually aperiodic – unlike every other crystal seen to date, this one was not periodic. It was different all throughout the crystal. He named the new form of matter ‘quasicrystals’ and published his results to mostly disbelief and ridicule. Linus Pauling said he was ‘talking nonsense’. However, over the years they were confirmed, and hundreds of other quasicrystals were discovered. There properties can be very unusual and are still being explored. Shactman would go on to win the Nobel prize for this discover in 2011.
So Penrose had gotten aperiodic tiling down to two tiles. Could it be done in one? This tile was pre-named the “Einstein tile”. Some of the sources I have read claim that although the name “einstein” conjures up the iconic physicist, it comes from the German ein Stein, meaning “one stone,” referring to the single tile.
But I don’t believe this. It’s too convenient.
The Einstein tile has finally been found. It has 13 sides, and is called “the hat”. Here it is again:
You’ll note that each tile is composed of eight ‘kite’ shapes, which are drawn in the faint lines to clarify them.
While the relationship between tiling and boardgames is obvious, as far as I know, there is only one board game based on Penrose tiling, called “Einstein” - this time definitely after the scientist.
I am guessing that there are other games out there that use Penrose tiles. Please let me (and everyone else!) know by leaving a comment.
I think this is a really fertile area for design, particularly now that a single aperiodic tile has been found. There are only certain ways that the patterns can be put together, and it would be interesting to try to block people, and build these spectacular patterns across the table. Think of a fractal version of Carcassonne. That would be awesome.
So game designers - get on it!

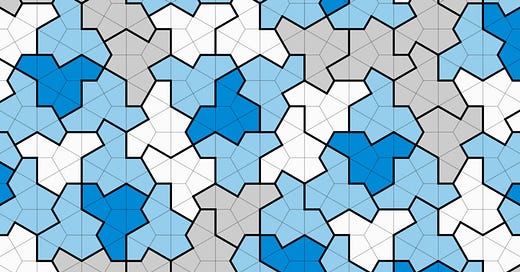


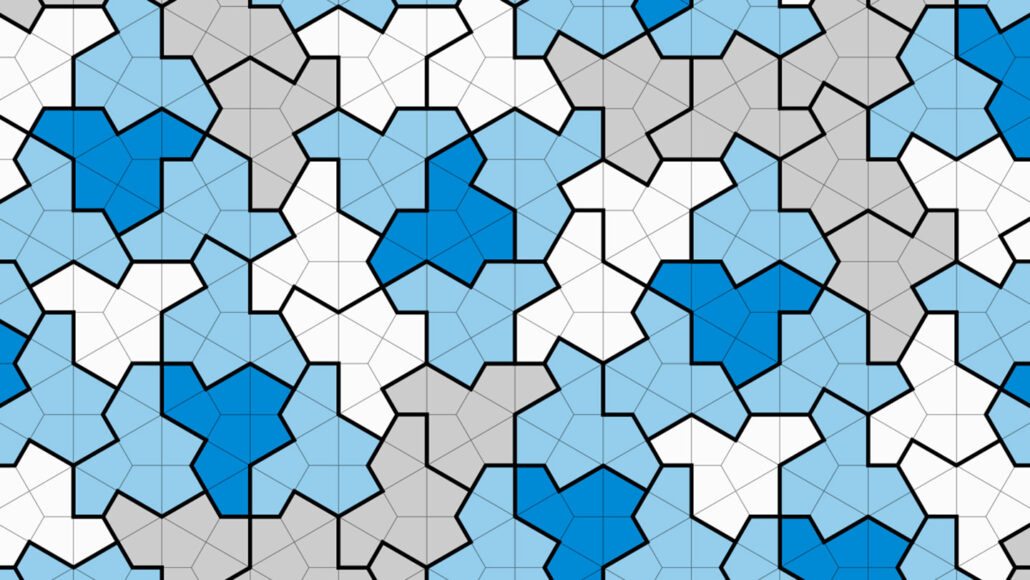




Chaos Tiles is a game (game system really, it comes with rules for two games) that uses two nonperiodic pieces.
While I haven't seen any commercial games that use Penrose tiles other than the one you mention, I did encounter a fellow designer who was fascinated with these (aren't we all?) who had a working prototype. It's been many years so I don't remember much of the mechanics, other than that you initially laid down a board of these tiles however you wanted, there were different colors on the tiles, and the core mechanic was collecting them (they had to engineer these little suction-cup-on-a-stick things to allow for collecting a single tile when it was surrounded by other tiles). When they reached out to Roger Penrose to ask if they could credit him, name the game "Penrose" in his honor, etc. - he said no. So... yeah, fertile ground for exploration: tile-laying, tile-collection, or even just as a way to build a random map of territories. And yeah, every game designer I know is inspired by this right now, and I suspect we'll either see a LOT of prototypes in the next few years, or we'll see none because everyone will be figuring that everyone else is doing it :D